선형회귀 분석은 독립 변수(independent)와 종속(dependent) 변수 간의 관계를 찾는 통계적 방법이다.
여기에 주중 총 학습 시간에 따른 학생들의 성적 상관 관계를 보여주는 데이터가 있다. 이 데이터 셋을 예로 들어 선형회귀분석에 대해 알아보자.
| 시간(Hours) | 성적(Marks) |
|---|---|
| 3 | 35 |
| 4 | 50 |
| 5 | 45 |
| 6 | 64 |
| 7 | 66 |
| 8 | 70 |
| … | … |
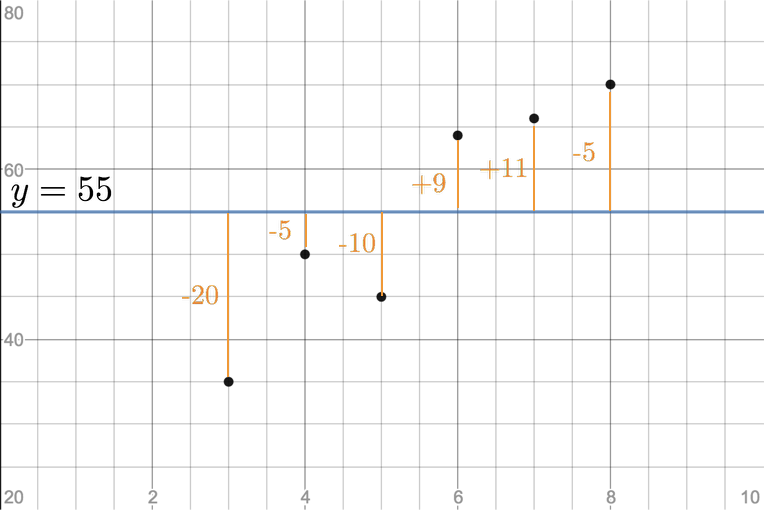
위 표에서 시간(Hours)는 독립 변수이고 성적(Marks)는 종속 변수이다. 유일한 종속 변수는 성적(Marks)이다. 다른 학생들의 성적을 예측할 수 있도록 주어진 데이터를 표현해야한다. 가장 좋은 방법은 평균값을 가진 1차 함수 그래프를 나타내는 것이다.
데이터 6개의 성적 평균 값은 $55((35+50+45+64+66+70)/2)$이다. 따라서 $y = 55$방정식을 직선으로 표현할 수 있다. 이 직선은 선형 회귀에 얼마나 잘 부합하는지 확인할 때 레퍼런스로 활용된다. 이 직선과의 거리를 비교하기 위해 '제곱 오류 합계(SSE: Sum of Squared errors)' 매트릭을 사용한다.
SSE(제곱 오류 합계) 계산하기
각 데이터 포인트에 대해, 실제 값 (예: $35$)과 예측 값 (평균값 : $55$)의 차이를 찾는다. 이 차이를 "오류(error)"(예: $35-55 = -20$)라고 한다. 그런 다음이 오류($(-20 * -20) = 400$)를 제곱한다. 제곱하는 이유는 서로 값의 차이를 높이면서 동시에 절대값을 만들어줌으로 서로 SSE를 비교하기 쉽기 때문이다.이 프로세스를 모든 데이터마다 반복한다. 그 다음으로 모든 데이터 포인트에 대해 계산된 모든 제곱 오류(squared error)를 합산한다. 그러면 SSE(Sum of Aquared Error; 제곱 오류 합계)가 된다.
| Hours | Marks | error=Marks-55 | $error^2$ |
|---|---|---|---|
| 3 | 35 | -20 | 400 |
| 4 | 50 | -5 | 25 |
| 5 | 45 | -10 | 100 |
| 6 | 64 | 9 | 81 |
| 7 | 66 | 11 | 121 |
| 8 | 70 | 15 | 225 |
| Avg=55 | SSE=952 |
따라서 SSE는 $952$가 된다.
독립 변수(Hours)를 사용해 선형 회귀 분석을 수행하여 최상의 결과를 얻은 후 SSE가 크게 감소해야한다. 만약 SSE 값이 커졌다면 데이터 셋에 부합한 일차함수식과 멀어진 것이다.
선형회귀는 직선의 방정식(Slope intercept form)인 $y = mx + b$을 사용한다. '$x$'는 독립 변수,'$m$'은 기울기, '$b$'는 $y$절편이다. SSE가 최솟값인 방정식의 해를 찾기 위해 '최소제곱법(OLS; Ordinary Least Squares)' 메서드를 사용한다.
최소제곱법(OLS; Ordinary Least Squares)
$\overline{y}=m\overline{x}+b$ 일차 방정식일 때, 최고제곱법의 기울기 $m$ 공식은 다음과 같다.
$m =\dfrac{\displaystyle\sum_{i=1}^n (x_i- \overline{x})(y_i- \overline{y})}{ \displaystyle\sum_{i=1}^n(x_i- \overline{x})^2}$
위 공식에서 $x_i$는 독립 변수(시간), $\overline{x}$는 독립 변수(시간)의 평균 , $y_i$는 종속 변수(성적), $\overline{y}$는 종속 변수(성적)의 평균이다.
각각 계산해보면 아래와 같이 나온다.
| Hours | Marks | $ x_i - \overline{x}$ | $y_i- \overline{y}$ | $ (x_i-\overline{x})(y_i-\overline{y})$ | $ (x_i-\overline{x})^2$ |
|---|---|---|---|---|---|
| x | y | $=x_i - 5.5$ | $=y_i - 55$ | ||
| 3 | 35 | -2.5 | -20 | 50 | 6.25 |
| 4 | 50 | -1.5 | -5 | 7.5 | 2.25 |
| 5 | 45 | -0.5 | -10 | 5 | 0.25 |
| 6 | 64 | 0.5 | 9 | 4.5 | 0.25 |
| 7 | 66 | 1.5 | 11 | 16.5 | 2.25 |
| 8 | 70 | 2.5 | 15 | 37.5 | 6.25 |
| $ \Sigma$=121 | $ \Sigma$=17.5 |
최소 제곱법 공식에 대입하여 계산해보면 $m=\frac{121}{7.5}$, 즉 $6.914$이다.
이제 일차 방정식의 $b$를 구하면 된다. $b=\overline{y}-m \cdot \overline{x}$으로, $b=55 - 6.914 \cdot 5.5 = 16.973$가 된다.
따라서 일차 방정식은 $y=6.914x+16.973$가 된다. 그래프를 다시 그려보자.
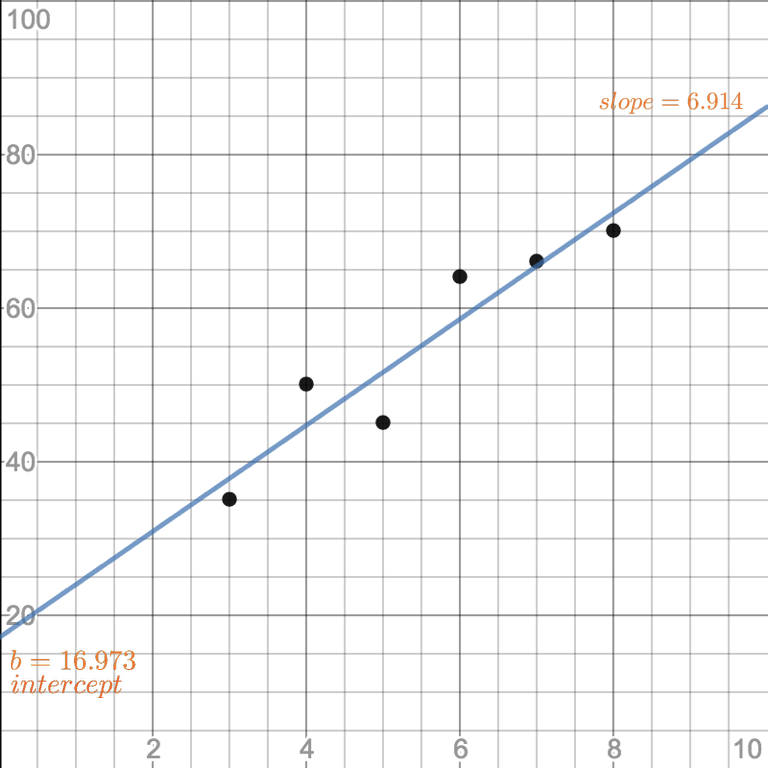
이제 이 방정식으로 SSE를 다시 계산해보자.
| Hours | Marks | 방정식 | error | |
|---|---|---|---|---|
| x | y | $y_p=6.194x + 16.973$ | $y - y_p$ | $error^2$ |
| 3 | 35 | 37.672 | -2.672 | 7.139584 |
| 4 | 50 | 44.586 | 5.414 | 29.3114 |
| 5 | 45 | 51.5 | -6.5 | 42.25 |
| 6 | 64 | 58.414 | 5.586 | 31.2034 |
| 7 | 66 | 65.328 | 0.672 | 0.451584 |
| 8 | 70 | 72.242 | -2.242 | 5.026564 |
| SSE=115.3 |
SSE가 $952$에서 $115.3$으로 오차가 감소했기 때문에 선형 회귀를 사용해 데이터 셋에 최적화된 방정식을 찾을 수 있게 된다.
이제 주중 총 22시간을 공부한 학생의 예상 성적을 유추할 수 있을 것이다.
자바스크립트 ES6 코드 구현
바닐라 ES6로 OLS(최소제곱법)를 사용한 선형회귀함수를 만들어보았다.
따로 math 라이브러리는 사용하지 않았으므로 배열 요소의 총 합(sum), 평균(average)를 구할 수 있는 간단한 utils 함수를 만들었다.
const utils = {
sum: (arr) => arr.reduce((total, amount) => total + amount),
avg: (arr) => utils.sum(arr) / arr.length
}
const LinearRegression = (data) => {
let
x_avg, // average of independent variable x
y_avg, // average of dependent variable y
num, // numerator : Sum of (xi - x)(yi - y)
den, // denominator : (xi - x)**2
m, // slope
b, // intercept
sse // the sum of squared error: sum of (y - (mx + b))
x_avg = utils.avg(data.x)
y_avg = utils.avg(data.y)
num = utils.sum(data.x.map((x, i) => (x - x_avg) * (data.y[i] - y_avg)))
den = utils.sum(data.x.map(x => ((x - x_avg) ** 2)))
if (num === 0 && den === 0) {
m = 0
b = data.x[0]
}
else {
m = num / den
b = y_avg - m * x_avg
}
sse = utils.sum(data.y.map((y, i) => (y - (m * data.x[i] + b)) * 2))
return {
slope: m,
intercept: b,
y: `${m}x + ${b}`,
SSE: `${sse}`
}
}
